The basic difference is that the odds ratio is a ratio of two odds (yep, it's that obvious) whereas the relative risk is a ratio of two probabilities (The relative risk is also called the risk ratio) Let's look at an example Relative Risk/Risk Ratio Suppose you have a school that wants to test out a new tutoring program The Relative Risk Ratio and Odds Ratio are both used to measure the medical effect of a treatment or variable to which people are exposed The effect could be beneficial (from a therapy) or harmful (from a hazard) Risk is the number of those having the outcome of interest (death, infection, illness, etc) divided by the total number exposed to Odds ratios approximate risk ratios when the outcome under consideration is rare but can diverge substantially from risk ratios when the outcome is common In this paper, we derive optimal analytic conversions of odds ratios and hazard ratios to risk ratios that are minimax for the bias ratio when outcome probabilities are specified to fall in

Relative Risk Odds Ratios Youtube
Hazard ratio vs odds ratio vs relative risk
Hazard ratio vs odds ratio vs relative risk-N = 905 6; A crude odds ratio can be converted to a crude risk ratio risk ratio = odds ratio/(1 − p0) (p0 × odds ratio), in which p0 is the outcome prevalence (risk) among the unexposed Some have applied this formula to an adjusted odds ratio to obtain an adjusted risk ratio 49 This method can produce biased risk ratios and incorrect confidence intervals 26 , 32




Relative Risk Odds Ratios Youtube
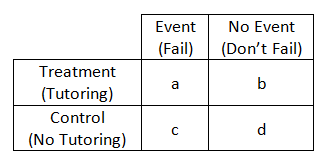
Relative risk, odds ratio and hazard ratio (and their confidence intervals) will be less than 10 If the converse holds true, these values will be greater than 10 Key words clinical trials, number needed to treat, odds, statistics (Aust Prescr 08;3112–16) IntroductionRelative Risk and Odds Ratio for the obese 3) Overall, you can see that decreasing the baseline incidence will decrease the odds ratio (300 in those who are nonobese versus 129 in those who are obese) Obviously, these results run counter to expected results, putting the onus on the researcher to justify them Similarly, you should findThe relative risk is different from the odds ratio, although the odds ratio asymptotically approaches the relative risk for small probabilities of outcomesIf IE is substantially smaller than IN, then IE/(IE IN) IE/IN Similarly, if CE is much smaller than CN, then CE/(CN CE) CE/CN Thus, under the rare disease assumption = () () = In practice the odds ratio is commonly used for
Odds ratio vs relative risk Odds ratios and relative risks are interpreted in much the same way and if and are much less than and then the odds ratio will be almost the same as the relative risk In some sense the relative risk is a more intuitive measure of effect sizeAbstract Odds ratios (OR) are commonly reported in the medical literature as the measure of association between exposure and outcome However, it is relative risk that people more intuitively understand as a measure of association Relative risk can be directly determined in a cohort study by calculating a risk ratio (RR)In a control group The odds ratio (OR) is the odds of an event in an experimental group relative to that in a control group An RR or OR of 100 indicates that the risk is comparable in the two groups A value greater than 100 indicates increased risk;
An odds ratio is simply the ratio of two sets of odds Increasing the odds ratio while holding a base odds constant corresponds to increasing the other odds, but may or may not be similar to the relative change in probability You may also want to ponder the difference between hazard and probability (see my earlier discussion where I make In this study Odds ratio is 93 which shows that the odds of having exposed to hormone replecement therapy is 9 times higher for cases compared to controls Odds ratios are not straight forward like percentage or relative risk but it has close approximation to themMeasures of relative effect express the outcome in one group relative to that in the other The risk ratio (or relative risk) is the ratio of the risk of an event in the two groups, whereas the odds ratio is the ratio of the odds of an event (see Box 92a) For both measures a value of 1 indicates that the estimated effects are the same for both interventions Neither the risk ratio nor the odds ratio




Hazard Ratio Relative Risk Or Odds Ratio Of Selected Outcomes For The Download Table
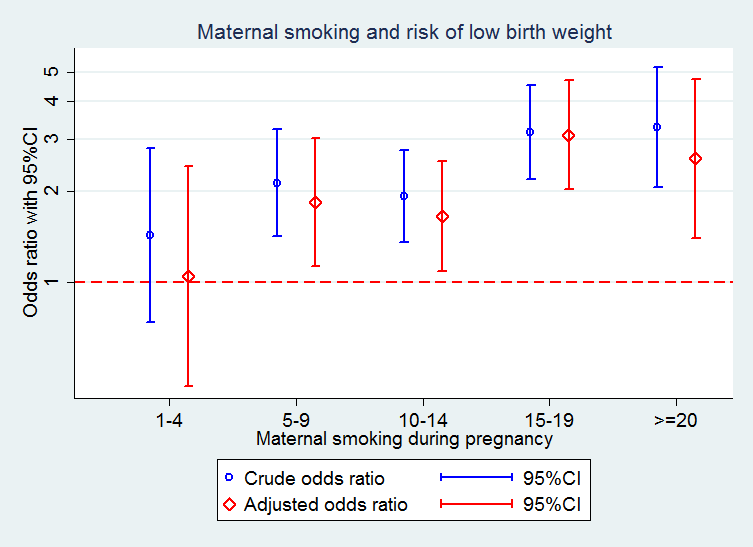



Medical Statistics And Data Science Statistics
The 95% CI is the interval that includes the 95% of risk ratios of these 100 population samples Thus, the 95% CI is the interval of values in which the true risk ratio is likely to lie with a probability of 95% To be statistically significant with a P For example, a relative risk of 15 would suggest a 50% increase in risk, whereas a relative risk of 05 would suggest a 50% decrease in risk Odds ratios The main difference between this and the other two measures is that there is no way of including aThe relative risk and the odds ratio are measures of association between exposure status and disease outcome in a population Relative risk In epidemiology, relative risk (RR) can give us insights in how much more likely an exposed group is to develop a certain disease in comparison to a nonexposed group Once we know the exposure and disease status of a research population,




Ktzum1llj5ibvm



Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia
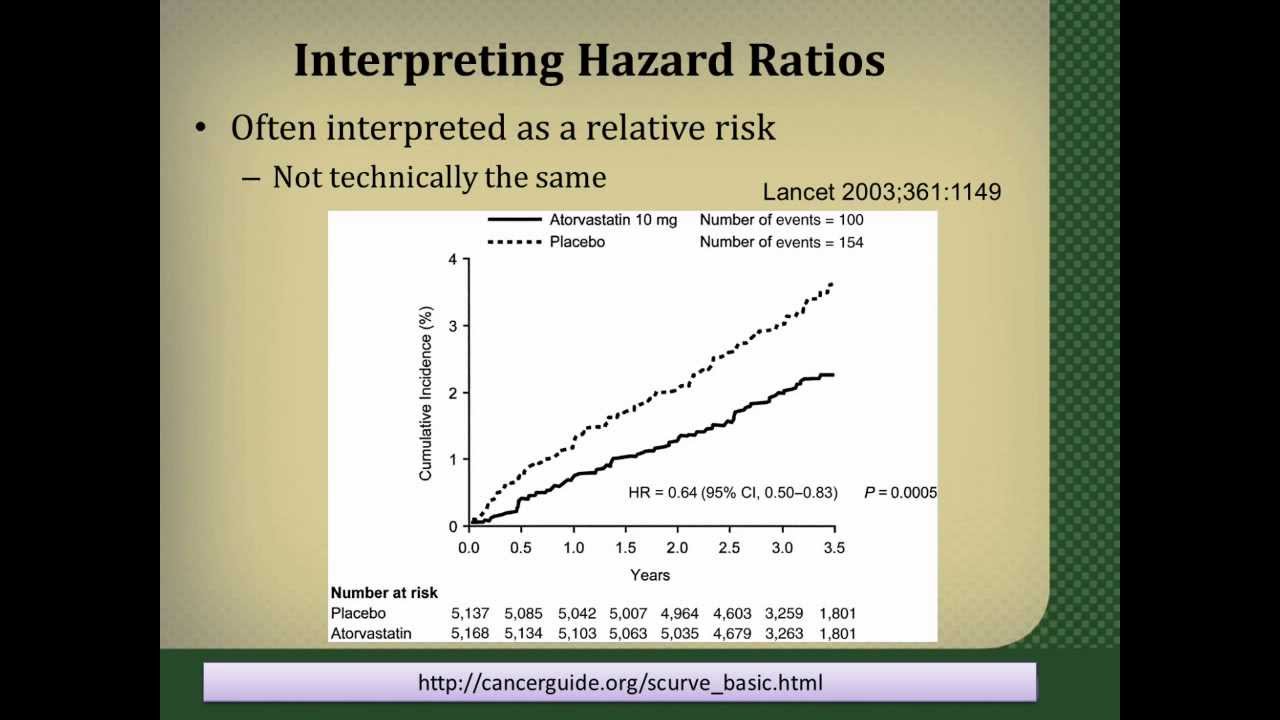
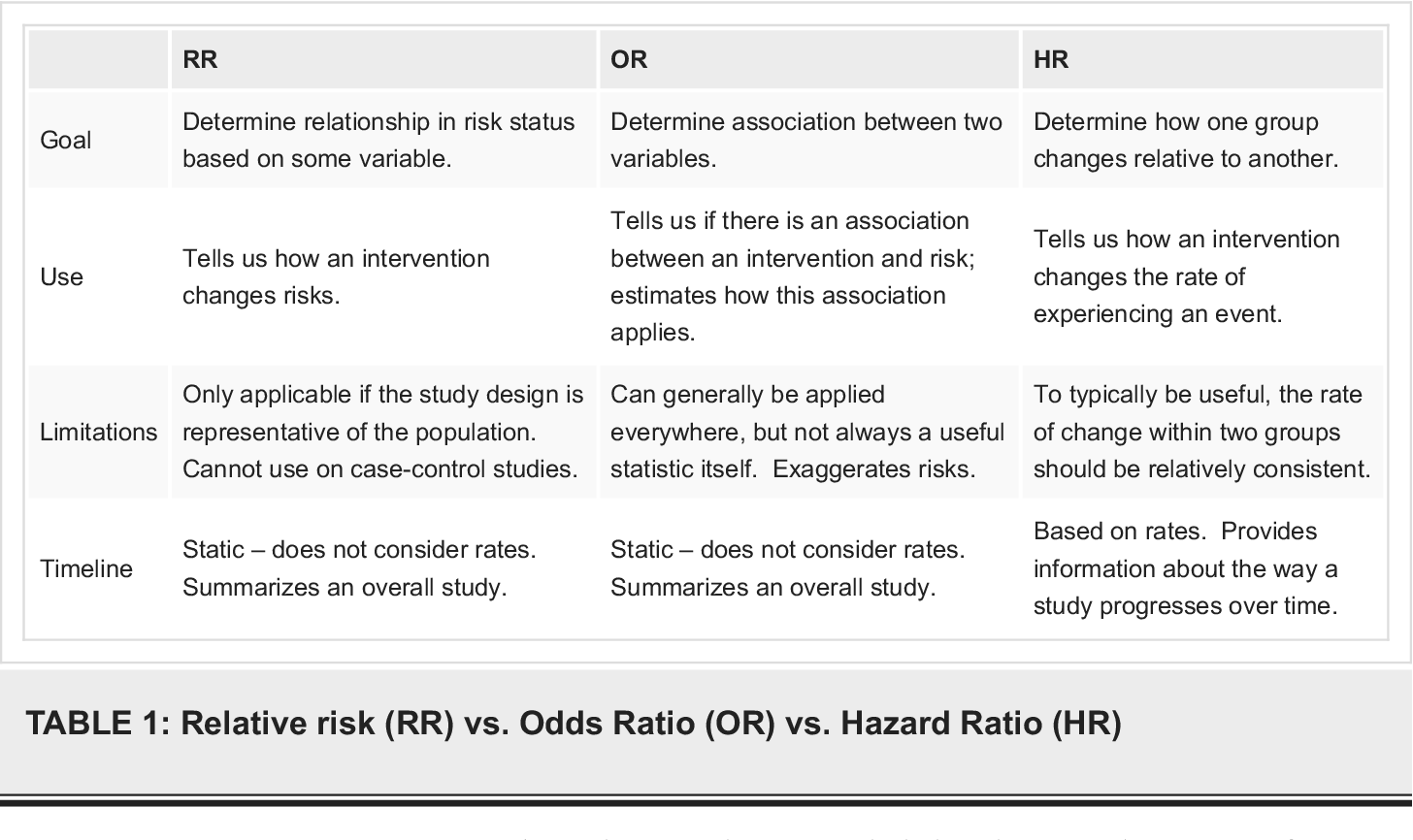
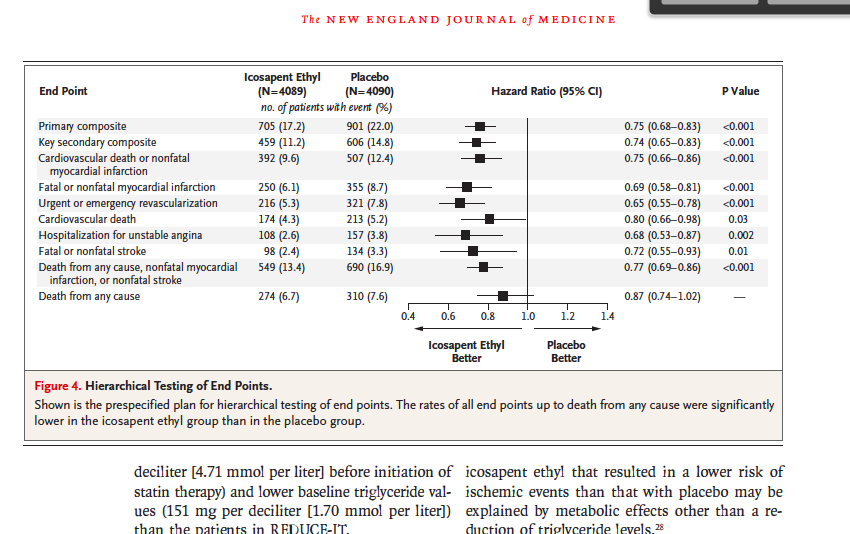
Hazard Ratios vs Risk Ratios (or Relative Risk) Hazard ratio is frequently interpreted as risk ratio (or relative risk), but they are not technically the same However, if that helps you to understand hazard ratio then it is OK But keep in mind HR is not RR hazard ratio vs odds ratio vs relative risk son of risks between groups, the ratio of risks, or the relative risk, is a statistic of choice Pooled HR was 161 (95% CI ;When the RR is exactly 1, the risk is unchanged For example, a report may state 'The relative risk of blindness in people given drug T was 15' This shows that the drug increased the risk of blindness Another measure that is used is the odds ratio For practical purposes, assume that the odds ratio is the same as the relative risk
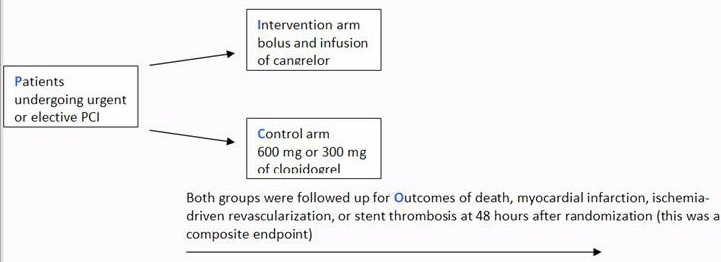



A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence
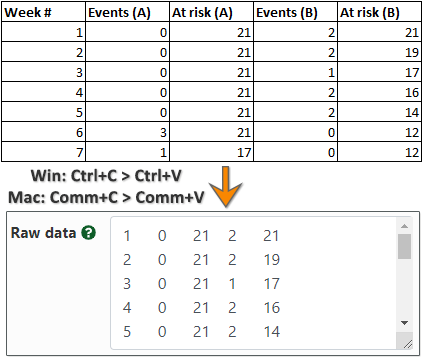



Hazard Ratio Calculator Calculate Hazard Ratio Hr Confidence Intervals P Value
3 studies) in the general populationThe risk difference of A relative to B is 001, the risk ratio is 101 Or one could view the risk ratio and the odds ratio as approximations to the hazard ratio or rate ratio Rates and hazards can exceed 1, unlike risks, so there's no constraint on the hazard ratio, unlike the risk ratioSometimes, we see the log odds ratio instead of the odds ratio The log OR comparing women to men is log(144) = 036 The log OR comparing men to women is log(069) = 036 log OR > 0 increased risk log OR = 0 no difference in risk log OR < 0 decreased risk Odds Ratio 0 5 10 15 More on the Odds Ratio Log Odds Ratio4 2 0 2 4




Odds Ratio Hazard Ratio And Relative Risk Janez Stare Semantic Scholar
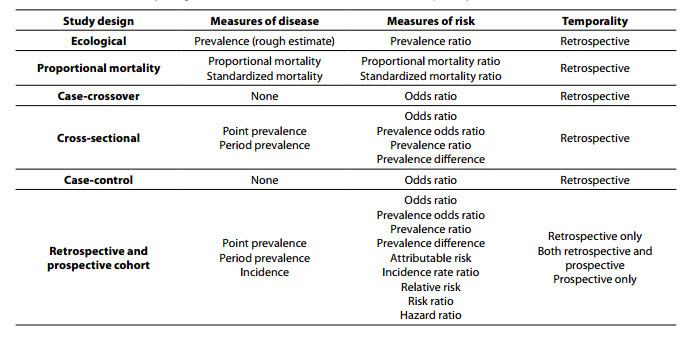



Observational And Interventional Study Design Types An Overview Biochemia Medica
This is not true for relative risk Switching the rows or columns inverts the odds ratio For example, the odds ratio for no cough given a history of bronchitis = (247/26)/(1002/44) = 0417 = 1/2397 This is the reciprocal of the OR for cough There are only two possible odds ratios, as switching both rows and columns givesOdds Ratio (OR) is a ratio or proportion of odds I just remember that odds ratio is a ratio of odds and probability isn't a ratio of odds (AKA it is the other option) Relative Risk = Probability / Probability Odds Ratio = Odds / Odds Now that you have a general idea of what odds ratio and relative risk are you need to know when to use A risk ratio of 10 indicates identical risk among the two groups A risk ratio greater than 10 indicates an increased risk for the group in the numerator, usually the exposed group A risk ratio less than 10 indicates a decreased risk for the exposed group, indicating that perhaps exposure actually protects against disease occurrence
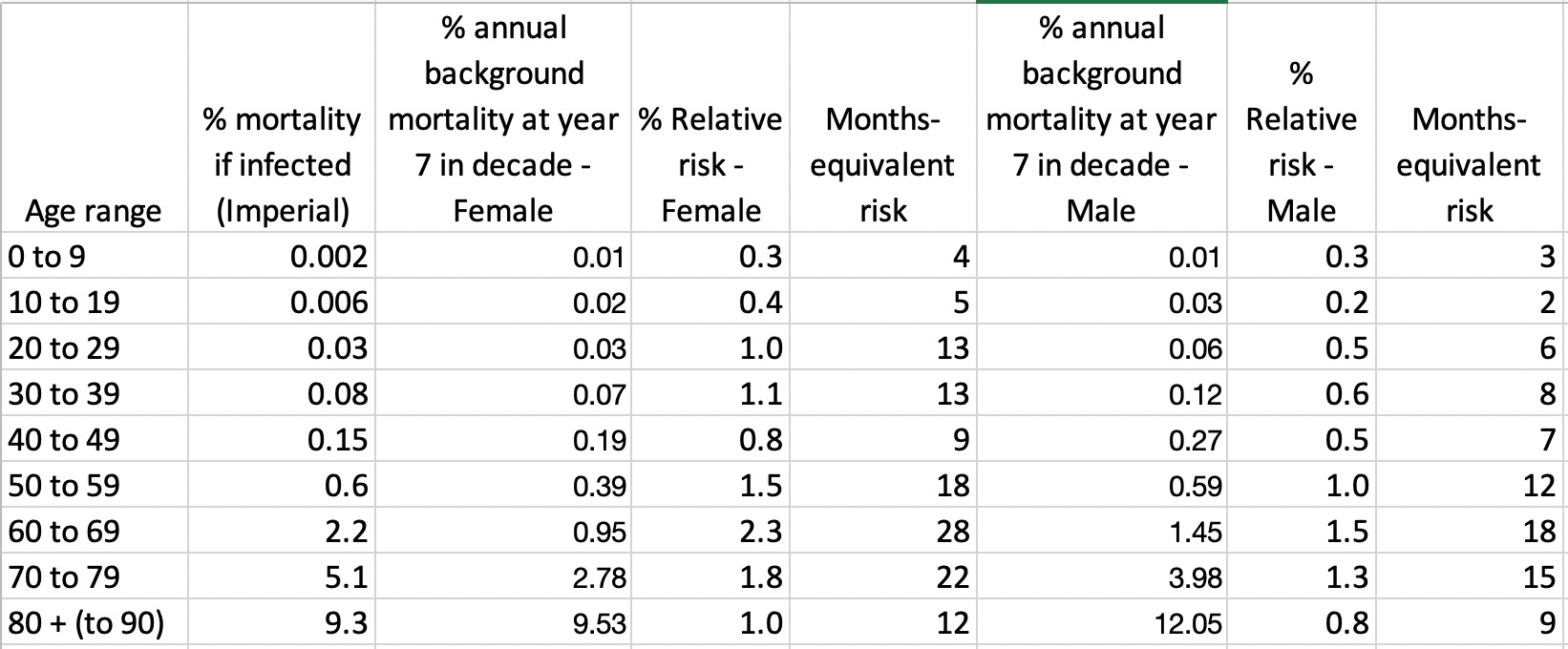



How Much Normal Risk Does Covid Represent By David Spiegelhalter Wintoncentre Medium




Odds Ratio Hazard Ratio And Relative Risk Janez Stare Semantic Scholar
Relative risks, odds ratios and hazard ratios?I2= 809%, P < 0001;When the disease is rare, the odds ratio will be a very good approximation of the relative risk The more common the disease, the larger is the gap between odds ratio and relative risk In our example above, p wine and p no_wine were 0009 and 0012 respectively, so the odds ratio was a good approximation of the relative risk OR = 0752 and RR = 075



Relative Risk Wikipedia
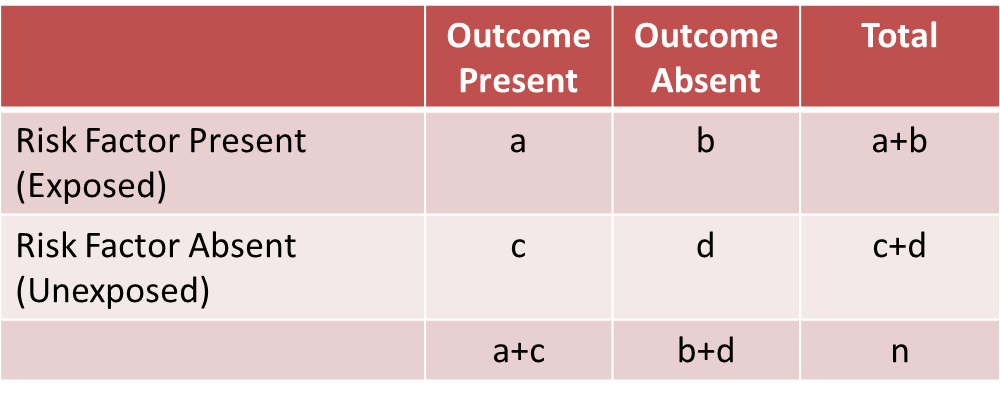



A Stratified Analysis
After converting the odds ratio to a risk ratio, the actual risk is 14 (mortality is 14 times more likely in patients with ICU delirium compared to those without ICU delirium) Because the incidence rate in the nondelirium group is high, the odds ratio exaggerates the true risk demonstrated in the studyIncludes the 95% of risk ratios of these 100 population samples Thus, the 95% CI is the interval of values in which the true risk ratio is likely to lie with a probability of 95% To be statistically significant with a Po005, a risk ratio should have a 95% CI not including 10 Thus, in the HOPE study, the risk ratio of 078 (95% CI 070–0 Risk ratios, odds ratios, and hazard ratios are three ubiquitous statistical measures in clinical research, yet are often misused or misunderstood in their interpretation of a study's results A 01 paper looking at the use of odds ratios in obstetrics and gynecology research reported 26% of studies (N = 151) misinterpreted odds ratios as risk ratios , while a
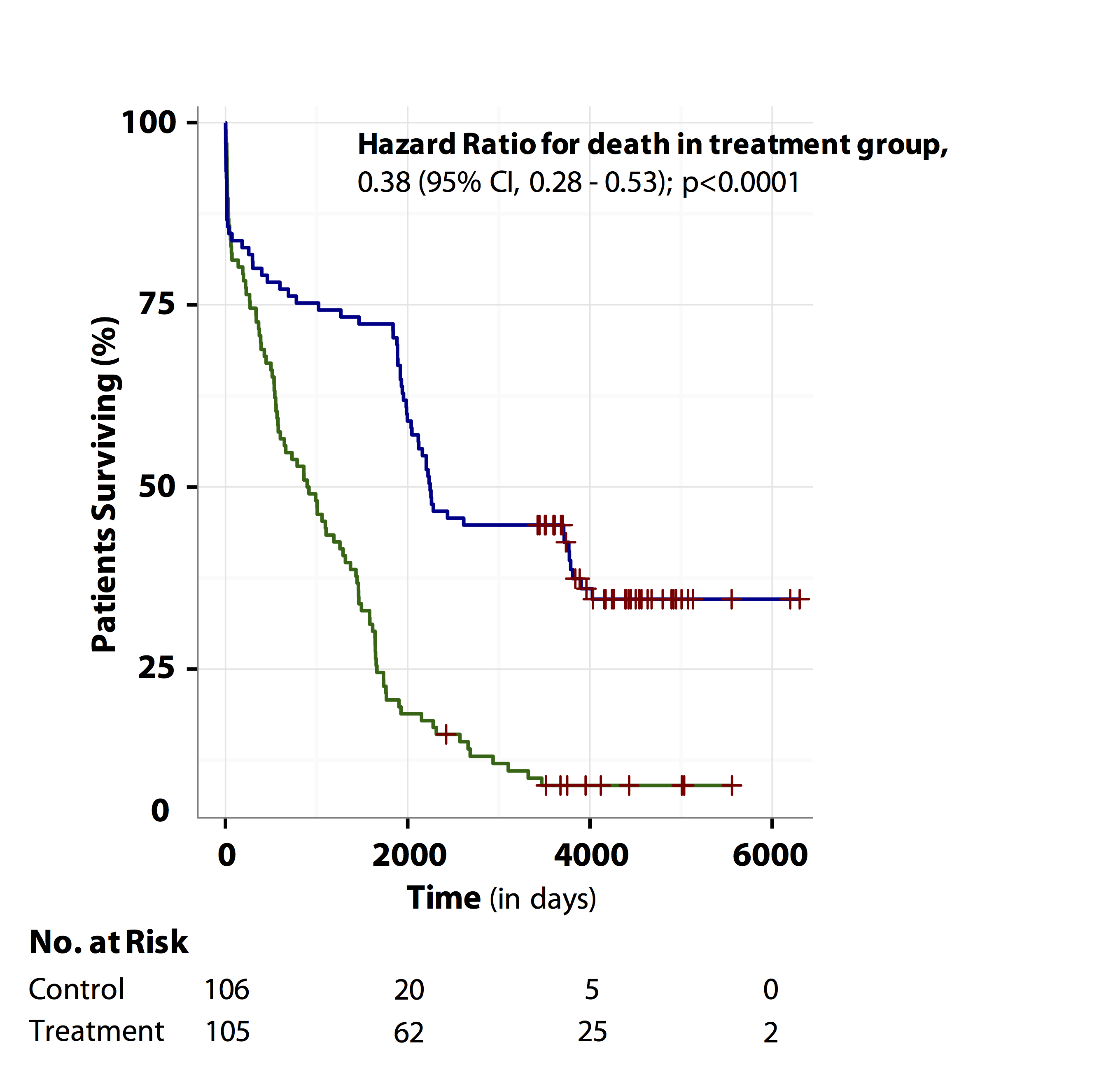



Tutorial About Hazard Ratios Students 4 Best Evidence




Hazard Ratio Odds Ratio Relative Risk And Increase In Hospital Download Scientific Diagram
Or one could view the risk ratio and the odds ratio as approximations to the hazard ratio or rate ratio Rates and hazards can exceed 1, unlike risks, so there's no constraint on the hazard ratio, unlike the risk ratio Hazard ratios / rate ratios can therefore be constant over the entire range of baseline hazard / background rate RogerRelative risks, odds ratio, hazard ratio relative risk/risk ratioratio of risk of an event occuring in the exposed group vs the unexposed grouprisk exposed risk unexposed RRN = 787 7;




Math3010 Week 6




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios
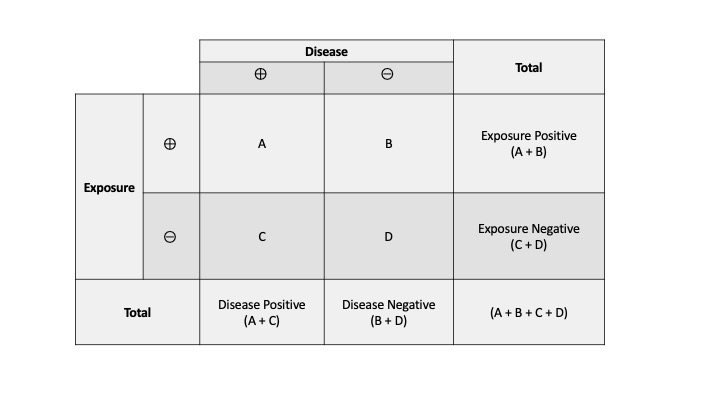
5 studies) in veterans, and 211 (95% CI , I2= 912%, P < 0001;A value lower than 100 indicates decreased risk The 95% confidence intervals and statistical The odds ratio (OR) is the ratio of the odds of cancer in smokers to the odds of cancer in nonsmokers OR = (a/b)/ (c/d) = (ad)/ (bc) The risk ratio (RR), also called the relative risk, is the ratio of the probability of cancer in smokers to the probability of cancer in nonsmokers Given that you know a, b, c, and d, you can compute either of




Relative Risk Odds Ratios Youtube



1
The hazard ratio would be 2, indicating higher hazard of death from the treatment Hazard ratios differ from relative risks (RRs) and odds ratios (ORs) in that RRs and ORs are cumulative over an entire study, using a defined endpoint, while HRs represent instantaneous risk over the study time period, or some subset thereof Hazard ratios suffer somewhat less from selection bias withPute either the odds ratio or the relative risk to answer this question The odds ratio compares the relative odds of death in each group For women, the odds were exactly 2 to 1 against dying (154/308 05) For men, the odds were almost 5 to 1 in favor of death (709/142 4993) The odds ratio is 9986 (4993/05) There is a 10fold greaterExcept for this difference the hazard ratio is expressed much in the same way as the relative risk A hazard ratio of 1 would indicate that there was no difference between treatments, whereas a hazard ratio of 2 would signify that the treatment group had twice the rate of an event, and a hazard ratio of 05 would signify that the treatment




How To Calculate Odds Ratio And Relative Risk In Excel Statology




Pdf Odds Ratio Hazard Ratio And Relative Risk
Relative Risk Risk is based on proportion of persons with disease = cumulative incidence Risk ratio = ratio of 2 cumulative incidence estimates = relative risk Since all of the measures are ratios, either of probabilities or of odds, it is clearer and simpler to use the word ratio in describing each type Odds ratio vs risk ratio You know the difference between risk and odds A risk is the proportion of subjects with an event in a total group of susceptible subjects Thus, we can calculate the risk of having a heart attack among smokers (infarcted smokers divided by the total number of smokers) and among nonsmokers (the same, but with nonLet us now look at the relation between the relative risk and the odds ratio (Zhang and Yu, 1998) OR= ˇ 1 1 1ˇ 1 ˇ 2 1 ˇ 2 = ˇ ˇ 2 1 2 1 1 = RR 2 1 (21) From this we see that OR is always further away from 1 than RR But, more importantly, we see that the odds ratio is close to the relative risk if probabilities of the outcome are small (Davies et al, 1998)




Relative Risk And Odds Ratio Usmle The Journey



How To Read A Forest Plot Cochrane Uk
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Percent increase = (Risk Ratio lower bound – 1) x 100 Percent decrease = (1 – Risk Ratio upper bound) x 100 It's worth stating again when comparing two proportions close to 1 or 0, the risk ratio is usually a better summary than the raw difference Odds Ratios We now turn to odds ratios as yet another way to summarize a 2 x 2 tableStart studying Applied Statistics Relative Risks, Odds Ratios, Hazard Ratios, NNT, NNH Part 1 Learn vocabulary, terms, and more with flashcards, games, and other




Pierfilippo De Sanctis Pfdesanctis Profile Pinterest




In A Meta Analysis Of Adjusted Estimates From Observational Studies Can I Pool Or With Hr And Rr Probably Not How Can I Transform Hr To Or
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe method of presenting the results of clinical studies can affect their interpretation by clinicians2 and nonclinicians alike3,4 Therefore, it is important to understand the different ways in which results can be presented Absolute risk refers to the simple event rate in a group of people whoWhere RR is the relative risk, OR is the odds ratio, and p is the control event rate, which leads to the following OR = ((1 p) * RR) / (1 RR * p) Thus, for instance, a RR of with a p of 01 would lead to an OR of 225, whereas if p increases to 02 it would lead to an OR of 267




Challenges In The Design And Interpretation Of Noninferiority Trials Insights From Recent Stent Trials Sciencedirect



Measures Of Association Stats Medbullets Step 1
Both the odds ratio and the relative risk compare the relative likelihood of an event occurring between two groups The relative risk is easier to interpret and is consistent with general intuition Some designs, however, allow only for the calculation of the odds For the majority of clinical trials, relative risk and odds ratio can be considered interchangeable as a measure of the relative change in the risk of a preventable event The hazard ratio is a related measure that weights the risk change according to The odds ratio will be greater than the relative risk if the relative risk is greater than one and less than the relative risk otherwise In the example above, if the adjusted odds ratio were interpreted as a relative risk, it would suggest that the risk of antibiotic associated diarrhoea is reduced by 75% for the intervention relative to the




Pdf What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios Semantic Scholar



Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia



How To Remember The Differences Between Odds Ratio Hazard Ratio And Likelihood Ratio And In What Instances They Should Be Applied Quora




Confidence Intervals And P Values




Odds Ratio Hazard Ratio And Relative Risk Janez Stare Semantic Scholar




What Is The Difference Between The Risk Ratio Rr And The Odds Ratio Or Quora



Interpreting Hazard Ratios Youtube




Evidence Of Safety Pooled Relative Risk Rr Or Odds Ratio Or And Download Table




Calculate Relative Risk With 95 Confidence Intervals




Measures Of Association Ppt Download




Odds Ratios And Risk Ratios Youtube




Hazard Ratio Relative Risk Or Odds Ratio Of Selected Outcomes For The Download Table



Relative Risk Ratios And Odds Ratios




Odds Ratio Hazard Ratio And Relative Risk Janez Stare Semantic Scholar




Epidemiologic And Research Applications In Community Nursing Lecture



How To Explain The Difference Between Hazard Ratio And Relative Risk To A Layman Quora




How To Interpret And Use A Relative Risk And An Odds Ratio Youtube




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Measures Of Association Ppt Download




Estimation Of Absolute Risk Of Colorectal Cancer Based On Healthy Lifestyle Genetic Risk And Colonoscopy Status In A Population Based Study Gastroenterology



Simple Way To Visualise Odds Ratios In R Stack Overflow




Measures Of Disease Association Ppt Download



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




Relative Risk Wikipedia



Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia




Pdf Data Analysis Of Epidemiological Studies Part 11 Of A Series On Evaluation Of Scientific Publications Semantic Scholar



Pdf What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios Semantic Scholar



Q Tbn And9gcqsrft9mxr7dpz7nmjrd2rigdx Ivp6aahq2v9iti13quuix7yw Usqp Cau




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1



State The Mean Median Hr Hazard Ratio Chegg Com




Hazard Ratio Relative Risk Or Odds Ratio Of Selected Outcomes For The Download Table




Nonproportional Hazards For Time To Event Outcomes In Clinical Trials Jacc Review Topic Of The Week Sciencedirect



2 Which Of The Following Is Not A Measure Of Relative Risk A B C D E Odds Ratio Risk Ratio Hazard Ratio Number Needed To Treat Rate Ratio Course Hero




Measures Of Association Ppt Download



How To Remember The Differences Between Odds Ratio Hazard Ratio And Likelihood Ratio And In What Instances They Should Be Applied Quora




Odds Ratio Litfl Ccc Research



1




Estimated Relative Risk Odds Ratio Or Hazard Ratio With 95 Ci For 4 Download Scientific Diagram



The Difference Between Relative Risk And Odds Ratios The Analysis Factor




Effect Sizes Basicmedical Key



Relative Risks And Odds Ratios What S The Difference Mdedge Family Medicine




Hazard Ratio Wikipedia



A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence




Measures Of Effect Relative Risks Odds Ratios Risk Difference And Number Needed To Treat Sciencedirect




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




Statistics For Gp And The Akt Sept 11



Plos One Bleeding Risk With Long Term Low Dose Aspirin A Systematic Review Of Observational Studies




Relative Risk Versus Odds Ratio Usmle Biostatistics 4 Youtube




How To Be Awesome At Biostatistics And Literature Evaluation Part Ii Tl Dr Pharmacy




What Does An Odds Ratio Or Relative Risk Mean



Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia




What Does An Odds Ratio Or Relative Risk Mean




Graphical Presentation Of Relative Measures Of Association The Lancet




Calculating The Risk Ratio Odds Ratio And Risk Difference In A Randomised Controlled Trial Youtube




Lincom Stata




Flowchart Of Study Selection Process Hr Hazard Ratios Or Odds Download Scientific Diagram
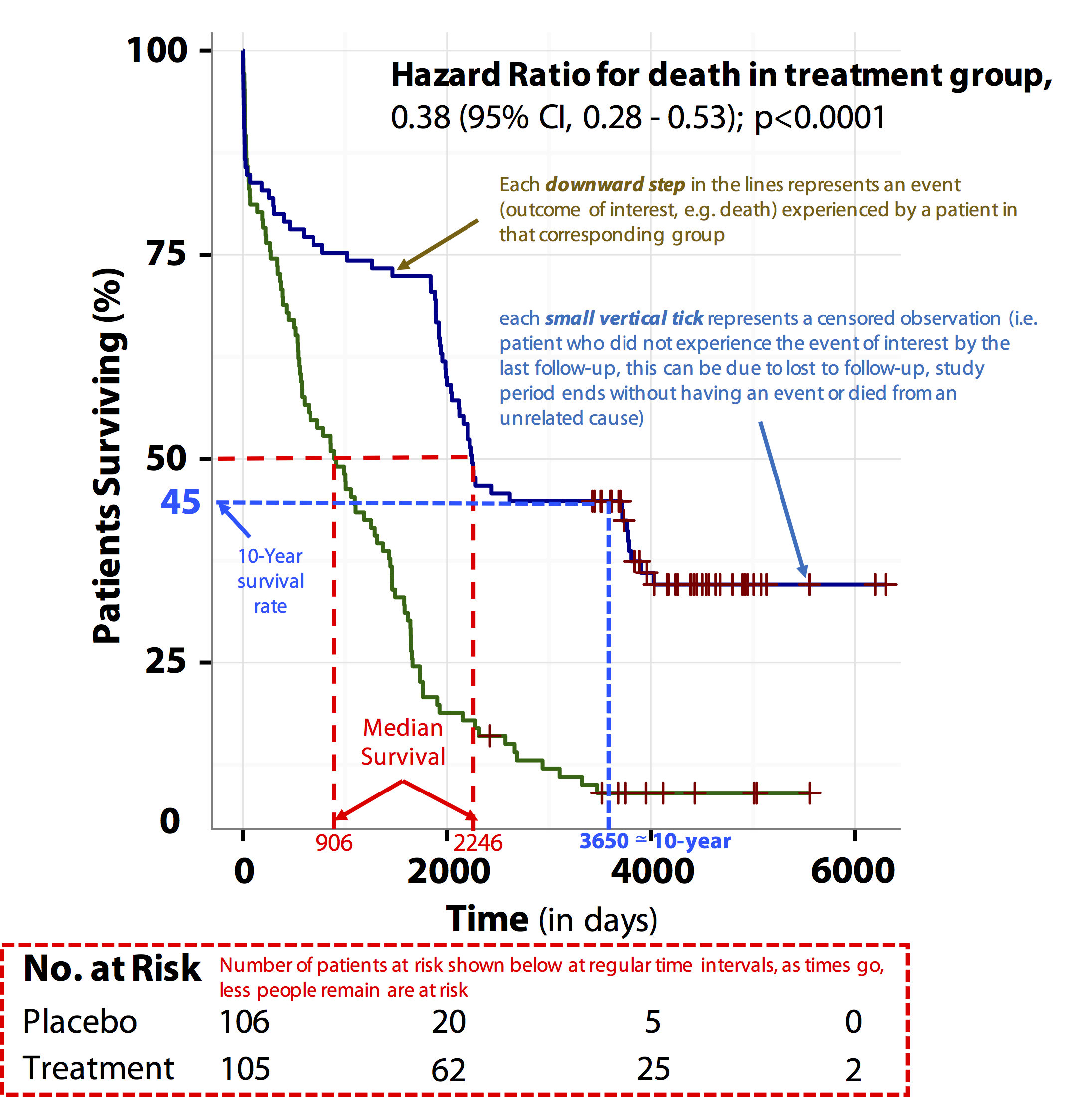



Tutorial About Hazard Ratios Students 4 Best Evidence




Odd Ratio Relative Risk Odds Ratio




Hazard Ratios




Chapter 6 Choosing Effect Measures And Computing Estimates Of Effect Cochrane Training
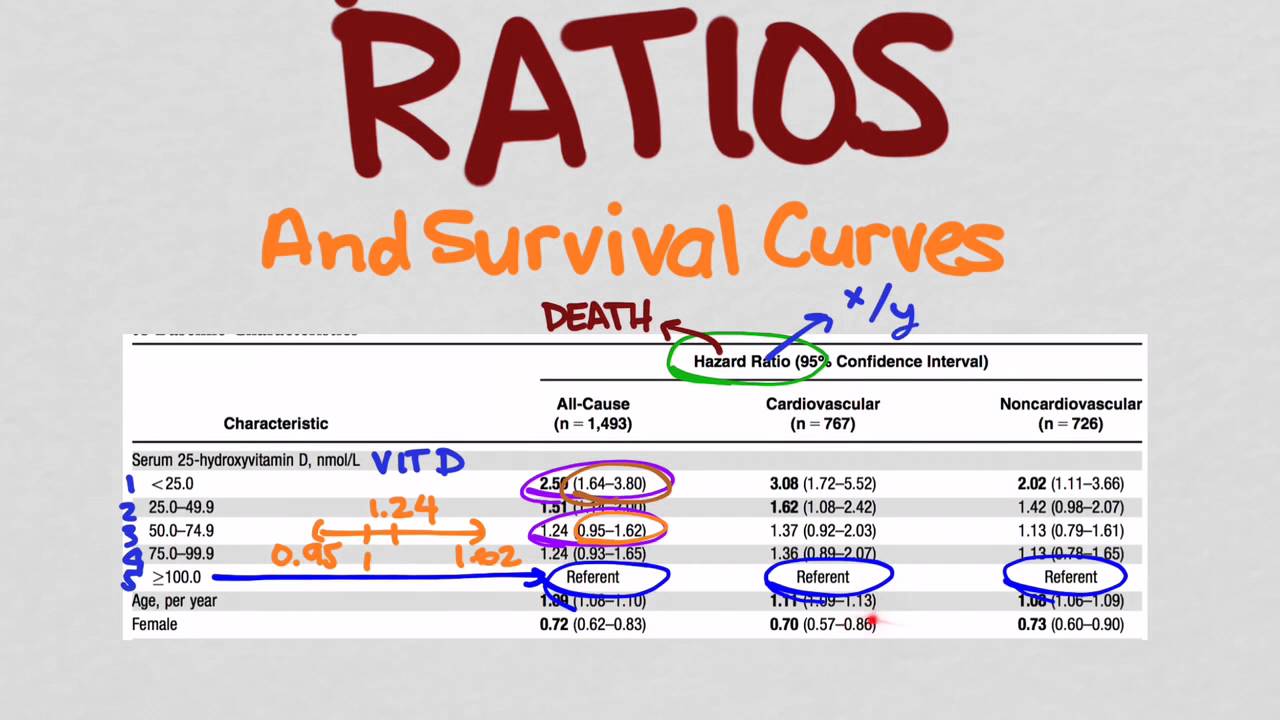



Hazard Ratios And Survival Curves Youtube




Statistics For Afp Dr Mohammad A Fallaha Afp
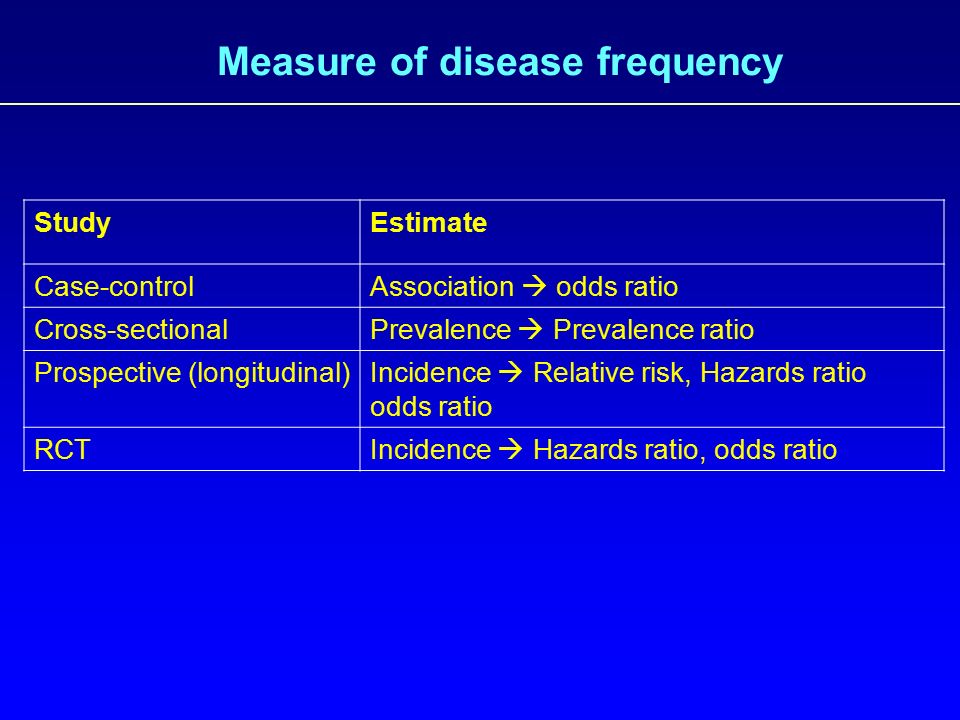



Design And Analysis Of Clinical Study Odds Ratio And Relative Risk Dr Tuan V Nguyen Garvan Institute Of Medical Research Sydney Australia Ppt Download




Odds Ratio Article




Understanding Systematic Reviews And Meta Analysis Archives Of Disease In Childhood




Eposters How Big Is A Big Hazard Ratio




Header Biostatistics And Epidemiology Lillian Sung Md Ph




1 Relative Risks Odds Ratios Or Hazard Ratios Of Risk Factors For Download Table
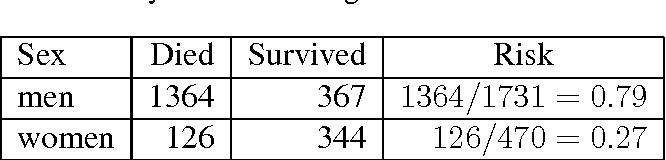



Odds Ratio Hazard Ratio And Relative Risk Janez Stare Semantic Scholar




Fillable Online Odds Ratio Hazard Ratio And Relative Risk Fax Email Print Pdffiller
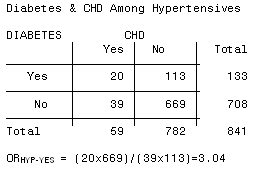



3 5 Bias Confounding And Effect Modification Stat 507
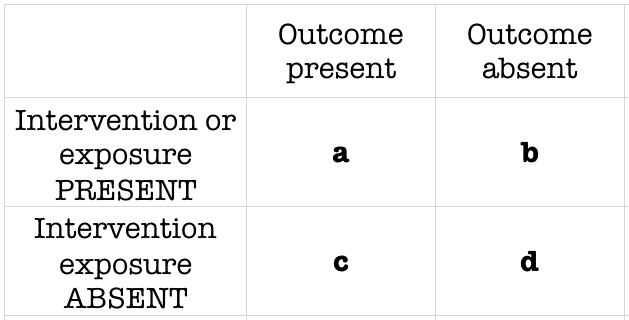



Odds Ratio Litfl Ccc Research




Pdf Odds Ratio Hazard Ratio And Relative Risk
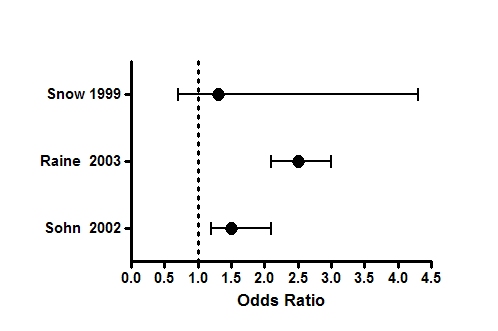



Graph Tip How Can I Plot An Odds Ratio Plot Also Known As A Forest Plot Or A Meta Analysis Plot Faq 809 Graphpad




Ppt Measures Of Association Powerpoint Presentation Free Download Id



Q Tbn And9gcs Pnxsjy3 X0gf842wm6tcfnesq2htc0kvu Tt2rst Svunqcb Usqp Cau




Lincom Stata




Relative Risk Odds Ratio Attributable Risk And



0 件のコメント:
コメントを投稿