The polar coordinates of a point are given Plot the point (6, π/2) 10 10 (6, π/2) (6, π/2) 10 5 10 10 10 10 6, /2) (6, π/2) 10 5 10 10 10 10L Find the corresponding rectangular coordinates for the point (x, y) = ( The polar coordinates of a point are givenMedium View solution The number of positive integral solutions of the equation Transcript Ex 33, 3 Prove that cot2 π/6 cosec 5π/6 3 tan2 π/6 = 6 Taking LHS cot2 π/6 cosec 5π/6 3 tan2 π/6 Putting π = 180° = cot2(180/6) cosec((5 ×180)/6) 3 tan2(180/6) = cot2 30° cosec (150°) 3tan2 30° Here, tan 30° = 1/√3 cot 30° = 1/tan〖30°〗 = 1/(1/√3) = √3 For cosec 150° , First, Finding sin 150° sin 150° = sin (180 – 30° ) = sin 30

Answer Preview Resultmessage Entered This Answer Is Chegg Com
Sin 1/2=π/6
Sin 1/2=π/6-Click here👆to get an answer to your question ️ Prove cot pi24 = √(2) √(3) √(4) √(6) ?Calculate sec(π/6) Determine quadrant Since our angle is between 0 and π/2 radians, it is located in Quadrant I In the first quadrant, the values for sin, cos and tan are positive Determine angle type 0 is an acute angle since it is less than 90°




7 T P 2 6 P 36frac Sec 2 Square Root Gauthmath
2, 5 x = 0, 6 x = π 2, 7 x = π Toc JJ II J I Back Section 4 Integrals 17 4 Integrals Formula for integration by parts R b a udv dx dx = uv − Measurements of pK a values, structural analyses, and computational studies revealed the presence of COOHπ interactions in 2,6diarylcarboxylic acids, 11 NHπ interactions in 2,6diarylpyridines, 12 cationπ interactions in 2,6diarylanilines, 13 and OHπ interactions in 2,6diarylphenols 10 Inspired by these precedents, here we report3 THE PARTIAL FRACTION EXPANSION OF sin2 x The identity (6) is a special case (x = r/2) of 1 1 _ _N1 sin2 x N2 2 sin2xk7r (9) This identity follows for N = 2 n in the same way as in Section 1, starting from sin2 x Writing it as 1 = 1 N/21 1 N2 _L xk sin x N2 k n 22xsin yields the partial fraction expansion of sin2 x in the limit
Y x √ abs round N randIn Figure 6, notice that if one of the acute angles is labeled as θ, θ, then the other acute angle must be labeled (π 2 − θ) (π 2 − θ) Notice also that sin θ = cos (π 2 − θ), sin θ = cos (π 2 − θ), which is opposite over hypotenuse5 EX 2 Convert the coordinates as indicated a) (8, π/4, π/6) from spherical to Cartesian b) (2√3, 6, 4) from Cartesian to spherical
Let f(x) = 3sin^4x 10sin^3x 6sin^2x – 3, x ∈ π/6, π/2 then f is (1) increasing in (π/2, π/2) (2) decreasing in (0,π/2) ← Prev Question Next Question → 1 voteSpelled out as "pi") is a mathematical constant, approximately equal to It is defined in Euclidean geometry as the ratio of a circle's circumference to its diameter, and also has various equivalent definitionsThe number appears in many formulas in all areas of mathematics and physicsThe earliest known use of the Greek letter π to represent the ratio of aSimplify (2pi)/ (pi/2) 2π π 2 2 π π 2 Multiply the numerator by the reciprocal of the denominator 2π 2 π 2 π 2 π Cancel the common factor of π π Tap for more steps Factor π π out of 2 π 2 π π ⋅ 2 2 π π ⋅ 2 2 π Cancel the common factor




Basel Problem Wikipedia
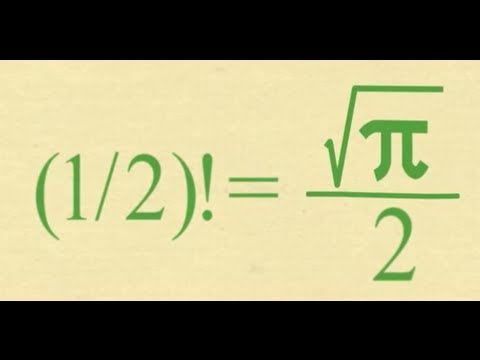



What Is The Factorial Of 1 2 Surprising 1 2 P 2 Youtube
(π)2 1− x2 (2π)2 1− x (3π)2 ··also has roots at x = 0,±π,±2π,±3π, Euler believed that these two functions are equivalent By Maclaurin series on sinx, we find that the coefficient of the x3 term = −1/6 On the other hand, for the infinite product, the coefficient of the x3 term = −I/π2 = − P∞ k=1 1/(k 2π2) ThusX 0 π 6 π 4 π 3 π 2 3 4 π π 3 2 π 2π yx=sin 0 05 2 2 ≈ 3 2 ≈ 1 2 2 ≈ 0 –1 0 yx=cos 1 3 2 ≈ 2 2 ≈ 05 0 −≈−2 2 –1 0 1 Now, if you plot these yvalues over the xvalues we have from the unwrapped unit circle, we get these graphsA most beautiful proof of the Basel problem, using lightHelp fund future projects https//wwwpatreoncom/3blue1brownAn equally valuable form of support is




Art Of Problem Solving
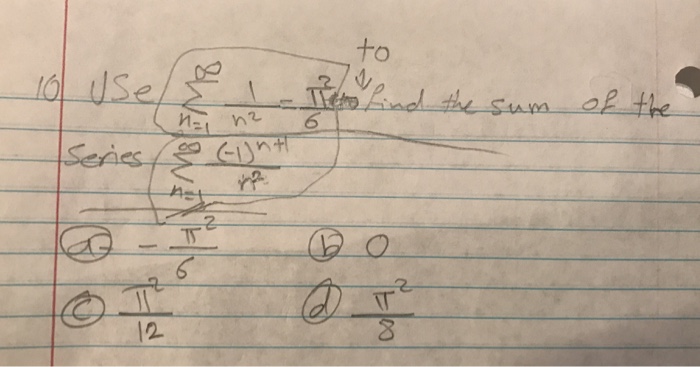



Use Sigma N 1 Infinity 1 N 2 Pi 2 6 To Find The Sum Chegg Com
π (6) Γ( )Γ( ) = Γ(x) 2 2 2x−1 The derivation and proof of these formulas can be found at 1 They are based on finding an approximation for Γ(x) in terms of an estimate for n!Polygon Calculator Use this calculator to calculate properties of a regular polygon Enter any 1 variable plus the number of sides or the polygon name Calculates side length, inradius (apothem), circumradius, area and perimeter Calculate from an regular 3gon up to a regular 1000gon Units Note that units of length are shown for convenienceThe number π (/ p aɪ /;




The Value Of Int Pi 2 Pi 2 Sin 2 X 1 2 X Dx Is




バーゼル問題 Wikipedia
Find the simplified form of cos13/5 cos x 4/5 sin x, x ∈ 3π/4,π/4 asked in Class XII Maths by nikita74 ( 1,017 points) inverse trigonometric functions1 rad = 180°/π = ° The angle α in degrees is equal to the angle α in radians times 180 degrees divided by pi constant α (degrees) = α (radians) × 180° / π or degrees = radians × 180° / π Example Convert 2 radians angle to degrees α (degrees) = α (radians) × 180° / π = 2 × 180° / = °Because of this the resulting boundary forces



The Number Of Values Of Theta In The Interval Pi 2 Pi 2 And Theta Pi 5 Is Youtube




Recall That The Fourier Series Of The Function F X Chegg Com
Modified equations and π^2/6 Mats Vermeeren (TU Berlin) Numerical discretizations of differential equations are often studied through their modified equation This is a differential equation, usually obtained as a power series, with solutions that exactly interpolate the discretizationδ=−π/2 Hence, wave 1 is RHC Similarly, Ee 2 =xˆ 2e jkz yˆ 2e jkz e −jπ/2 Wave 2 has the same magnitude and phases as wave 1 except that its direction is along −ˆz instead of zˆ Hence, the locus of rotation of E will match the left hand instead of the right hand Thus, wave 2 is LHCThe Value of Cos 2 ( π 6 X ) − Sin 2 ( π 6 − X ) is CBSE CBSE (Arts) Class 11 Textbook Solutions 7909 Important Solutions 12 Question Bank Solutions 6916 Concept Notes & Videos 365 Syllabus Advertisement Remove all ads The Value of Cos 2 ( π 6 X ) − Sin 2 ( π 6 − X ) is




Fourier Serie Property For Sum N 1 Infty Frac 1 N 2 Frac Pi 2 6 Mathematics Stack Exchange




Tan Pi 2 X Tan Pi 2 Theta Youtube
The beta function (also known as Euler's integral of the first kind) is important in calculus and analysis due to its close connection to the gamma function, which is itself a generalization of the factorial function Many complex integrals can be reduced to expressions involving the beta function The recurrence relation of the beta function is given by pi/6 radians is 30 degrees A radian is the angle subtended such that the arc formed is the same length as the radius There are 2pi radians in a circle, or 360 degrees Therefore, pi is equal to 180 degrees 180/6=303 Solution Since f(z) = ez has an antiderivative F(z) = ez everywhere in C, the integral is independent on the path and Z C ez dz = e3 2 πe i 3π 2 −e 2 e i π 2 = e−i3π 2 −ei π 2 = i−i = 0




Basel Problem Wikipedia




Lim X Pi 2 Secx Tanx
The solution of the equation sin1 6x sin1 6 √3 x = (π/2) is (A) (1/12) (B) 12 2 (D) (1/6) Check Answer and Solution for above qThe depth is modeled by the function D (t) = 5 sin (π 6 t − 7 π 6) 8, D (t) = 5 sin (π 6 t − 7 π 6) 8, where t t is the number of hours after midnight Find the rate at which the depth is changing at 6 2 e^x (hyperbolic functions included), sin x, cos x, tan x all have a factorial in their power series The only useful examples I can think of that don't have a factorial are the inverse trig functions and the natural log Anyways, I don't want to get into an argument, I'll just rephrase myself, most power series that I've seen and
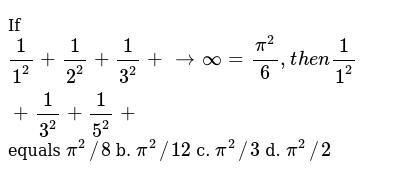



If 1 1 2 1 2 2 1 3 2 Tooo Pi 2 6 T H E N1 1 2 1 3 2 1 5 2 Equals Pi 2 8 B Pi 2 12 C Pi 2 3 D Pi 2 2




7 T P 2 6 P 36frac Sec 2 Square Root Gauthmath
51 Approximating and Computing Area 3 2 25 3 35 4 45 5 5 10 15 25 30 x x 2x−2 2 25 3 35 4 45 5 5 10 15 x x x−2 6 Let f (x) = cos x (a) Calculate R 4 and L 4 for the interval 0, π 2 (b) Sketch the graph of f and the rectangles that make up each of the approximations (c) Is the area under the graph larger or smaller than R 4?ThanL 4? Transcript Ex 33, 2 Prove that 2sin2 π/6 cosec2 7π/6 cos2 π/3 = 3/2 Taking LHS 2sin2 π/6 cosec2 7π/6 cos2 π/3 Putting π = 180° = 2 sin2 180/6 cosec2 (7 ×180)/6 cos2 180/3 = 2sin2 30° cosec2 210° cos2 60° = 2(sin 30°)2 (cosec 210°)2 (cos 60°)2 Here, sin 30° = 1/2 & cos 60° = 1/2 For cosec 210° , lets first calculate sin 210° sin 210° = sin (180 30) = −sin =tan (4π/2π/6) clearly, the angle lies in IV quadrant in which tangent function is negative and the multiple of π/2 is even =tan (4π/2π/6)= cot (π/6) =1/√3 (iv) cos (25π/4) Solution The cosine function is an even function, Therefore, cos (25π/4)=cos (25π/4)




These 27 The Maximum Value Of Sin Left Theta Frac Pi 6 Right Cos Left Theta Frac Pi 6 7 Right Attained At Theta In 0 Pi 2 1 Frac Pi 18 2 Frac Pi 6
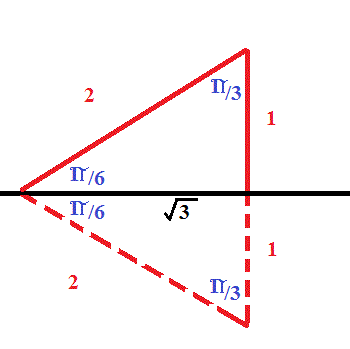



How Do You Find The Exact Value Of Tan Pi 6 Socratic
2 π Z π 0 f(x)cosnxdx = 2 π Z π 0 xcosnx dx If n = 0, then a0 = 2 π Z π 0 x dx = π, and if n ≥ 1, then integrating by parts, one finds that 2 π Z π 0 xcosnx dx = 2 π xsinnx n − 2 nπ Z π 0 sinnx dx = 2 n2π cosnx π 0 = 2 n2π (−1)n − 1 Hence an = 0 if n is even and an = − 4 n2π when n is odd, and hence f(x) ∼ π 2 The maximum value of sin (x π/6) cos(x π/6) in the interval (0, π/2) is attained at (a) x = π/12 (b) x = π/6 (c) x = π/3 (d) x = π/2ρ > 3 π G P 2 = 3 π 667 × 108 dyne cm 2 gm2 (13 s) 2 ≈ 10 8 g cm3 This limit is just consistent with the known densities of white dwarf stars But soon the faster ( P = 0033 s) pulsar in the Crab Nebula was discovered, and its period implies a




Ex 3 3 6 Prove That Cos Pi 4 X Cos Pi 4 Y Chapter 3




Prove Without Calculus Sigma 1 N 2 Pi 2 6 Maths Doubts Goiit Com
6003 Homework #10 Solutions / Fall 11 2 2 Inverse DT Fourier Series DeterminetheDTsignalswiththefollowingFourierseriescoefficients Assumethatthe(511), in this case we obtain p ren i = δ iθ 8 π 2 ρ 3 bracketleftbigg 7 π 4 8 α 4 480 α 4 − parenleftbigg ξ − 1 6 parenrightbigg π 2 2 α 2 α 2 bracketrightbigg (522) We notice that also in this case the parameter ξ appears in the final expression for the renormalized pressure;F0 changes from negative to positive at x = π/2 so, by the first derivative test, the local minimum value of f is f(π/2) = cos2(π/2)−2sin(π/2) = 02 −2(1) = −2 f0 changes from positive to negative at x = 3π/2 so, by the first derivative test, the local maximum value of f is



When Solving Sin X 1 2 The First Solution Is Pi 6 Why It Is Converted To 11pi 12 And How Quora




Basel Problem Wikipedia
The benchmark angle measures (as defined by the College Board) are 0, ${π}/{6}$, ${π}/{4}$, ${π}/{3}$, ${π}/{2}$ radians which are equal to the angle measures 0°, 30°, 45°, 60°, and 90°, respectively You need to be able to use these with the trigonometric functions described in the above trigonometry section (sine, cosine, and tangentJoin / Login maths Prove cot 2 4 π = 2 3 4 6If tan − 1 a a x tan − 1 a a − x = 6 π , then x 2 =?




Basel Problem Wikipedia



The Home Of Whole Pi
7 Consider f (x) = 5x on 0,3 (a854 x 180/ π = 4502 degrees814 x 180/ π = – 4666 degrees π/180 x 180/ π = 1 degree Example 8 Convert the angle π /5 radians into degrees Solution Angle in radian x 180/ π = Angle in degrees By substitution, π /5 x 180/ π = 36 degrees Example 9 Convert the angle – π /8 radians into degrees Solution1/k 2 = π 2/6 P A short elementary proof of Daniel Daners∗ The University of Sydney, NSW 06, Australia danieldaners@sydneyeduau Revised version, Abstract P∞We give 2 a short elementary proof of the well known identity ζ(2) = 2 k=1 1/k = π /6




If The Sum Of All The Solutions Of The Equation 8 Cosx Cos Pi 6 X Cos Pi 6 X 1 2 1 In 0 Pi Is K Pi Then K Is Equal To
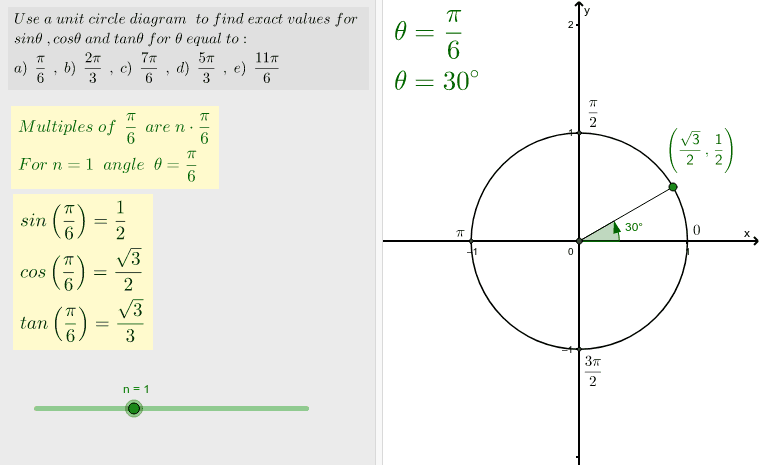



Multiples Of P 6 Geogebra
1 2 3 π sin asin 4 5 6 − e cos acos exp ← 7 8 9 × g tan atan ln, • 0 E ∕ R rad deg log(a,b) ans;4 The Sine and and Gamma Functions To derive the sine product formula, we first find a relationship beRadians × (180/π) = Degrees Example 2 Convert π/6 into degrees Solution Using the formula, π/6 × (180/π) = 180/6 = 30 degrees Radian to Degree Equation As we know already, one complete revolution, counterclockwise, in an XY plane, will be equal to 2π (in radians) or 360° (in degrees) Therefore, both degree and radian can form an
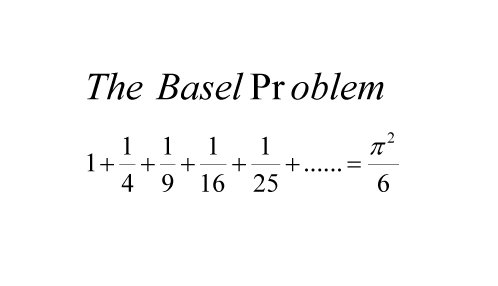



Fermat S Library Paper An Easy Way To Prove That 1 1 4 1 9 1 16 P 2 6 Which Euler Missed Read Here T Co Ew5uiclgy7




Computing Series Sum N 1 Infty 1 N 2 Using Fourier Series Mathematics Stack Exchange
Can you remember 100 digits of pi?The MUSCLE Song (Memorize Your Anatomy) https//youtube/VmcQfCcGScYOUR PODCAST http//sidenotepodcastcomGet the song!Question Find The Distance Between (2,π/6,0) And(1,π,2) , Where Points Are Given In Cylindrical Coordinatesans) 353 This problem has been solved! ∴ f(x) is not strictly decreasing in any of the intervals (0, 1), (\(\frac { π }{ 2 }\), π) and (0, \(\frac { π }{ 2 }\)) Question 14 Find the least value of a such that the function f given by f (x) = x² ax 1 is strictly increasing on (1, 2)




Pi 2 62 2 Pi 3 2 Find Out




Fourier Serie Property For Sum N 1 Infty Frac 1 N 2 Frac Pi 2 6 Mathematics Stack Exchange
Cosine calculator online cos(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads



Which Is Equivalent Sin 1 Cos Pi 2 Give Your Answer In Radian




But How Did Euler Do It A Beautiful Solution To The Famous Basel Problem Youtube



Biomath Trigonometric Functions




Problem 7 2 Points Suppose That Ffrac P 2 6 A Gauthmath




Divergence Of The Sum Of The Reciprocals Of The Primes Wikipedia




Plot Of E L L P 2 6 Versus L For The State I 1 0 1 2 Of The Download Scientific Diagram




Basel Problem Wikipedia



What Is Math Dfrac 1 1 2 Dfrac 1 2 2 Dfrac 1 3 2 Dfrac 1 4 2 Math Quora



If A 0 P 6 P 4 P 3 P 2 And F A B Is A Surjection Defined By F X Cos X Then Find B Sarthaks Econnect Largest Online Education Community




Basel Problem Wikipedia




By Euler S Methods Derive The Summation Pi 2 8 Chegg Com
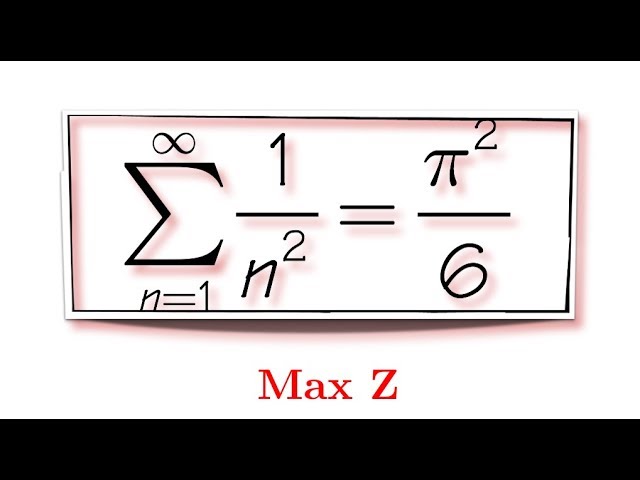



Proof By Intuition Done By Leonhard Euler Sum Of 1 N 2 Feat Max Youtube




Ex 5 1 26 Find Values Of K So That F X K Cos X Pi 2x




Fermat S Library בטוויטר New Paper A Proof That Euler Missed Solving The Basel Problem The Easy Way 1 1 4 1 9 1 16 P 2 6 Proof Here T Co Ew5uid3imh T Co Lcmxulqevh
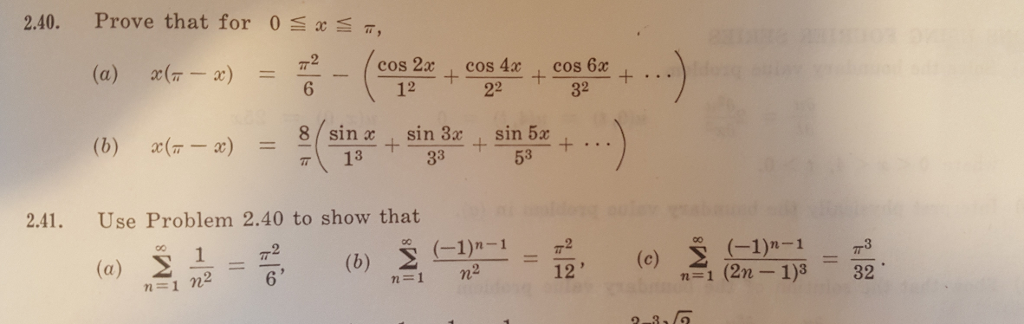



Prove That For 0 X Pi A X Pi X Pi 2 6 Chegg Com




Ex 3 3 6 Prove That Cos Pi 4 X Cos Pi 4 Y Chapter 3




2 H X Vs X And Lim X 2 H X P 2 6 Download Scientific Diagram



Important Angles Ppt Download




Ex 3 3 2 Prove 2 Sin2 Pi 6 Cosec2 7pi 6 Cos2 Pi 3 3 2




Solve The Equation On The Interval 0 2 Pi Cos 2 X Chegg Com




Answer Preview Resultmessage Entered This Answer Is Chegg Com




Here Is Euler S Idea To Obtain The Formula 1 1 2 2 Chegg Com



The Expression 3 Sin 4 3p 2 A Sin 4 3p A 2 Sin 6 P 2 A Sin 6 5p A Is Equal To Sarthaks Econnect Largest Online Education Community




Assume The Fact That 1 1 2 2 1 3 2 1 4 2 Chegg Com
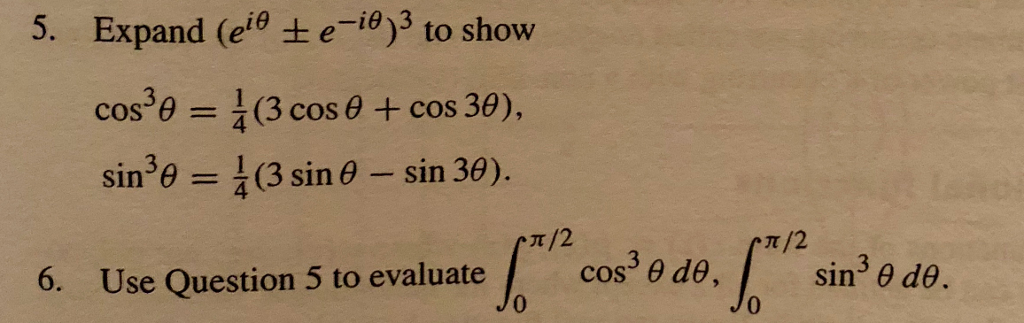



Expand Ei T E 3 To Show Cos38 Sin38 Use Question Chegg Com



If Sigma Infinity N 1 1 N 2 Pi 2 6 Then Find Chegg Com




Problem 7 1 N N N Determine The




Euler S Calculation Of The Sum Of The Reciprocals Of The Squares A Mini Primary Source Project For Calculus Ii Students Mathematical Association Of America




1 Cos X Y Underline 2 Cos X Y Underline 3 Cos Gauthmath




Show That The Sum Of The Series Sigma N 1 Infinity Chegg Com




6 Tan Left Frac 2 3 Theta Right Sqrt 3 Then Theta Is 1 Pi Pi Overline 2 Frac 6 6 3 Frac 3 N Pi 2 Frac Pi 4 2 N 4 Frac 3 N Pi 2



Suppose F X 2 Cos X F0 10 F P 2 6 If Fx Is An Gauthmath



1




Solve Sin 1 1 X 2 Sin 1 X Pi 2 Then X Is Trigonometry Mcq




Particular Values Of The Riemann Zeta Function Wikipedia




A 0 5 Pi 2 Times 5 12 3 Mathrm Cm Mathrm S 2 I 2 X 2 0 5 Pi Sqrt 5 2 3 2 Pm 6




Rightarrow Sin Left Cos Left Frac Pi 2 Frac Pi Pi 6 Right Right Sin Left Sin Left Frac 6 Pi 14 Pi 12 Right Right



Are There Any Visual Proofs For Sum N 1 Infty Frac 1 N 2 Frac Pi 2 6 Newbedev
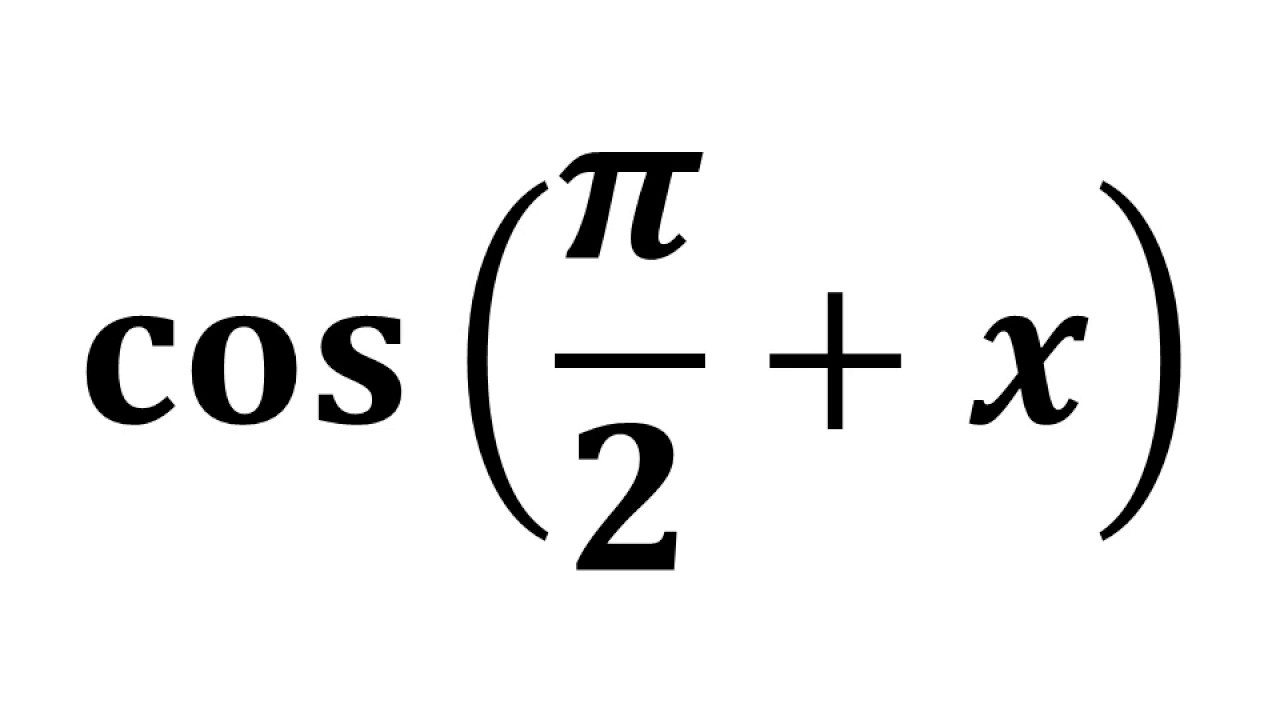



Cos Pi 2 X Cos Pi 2 Theta Youtube
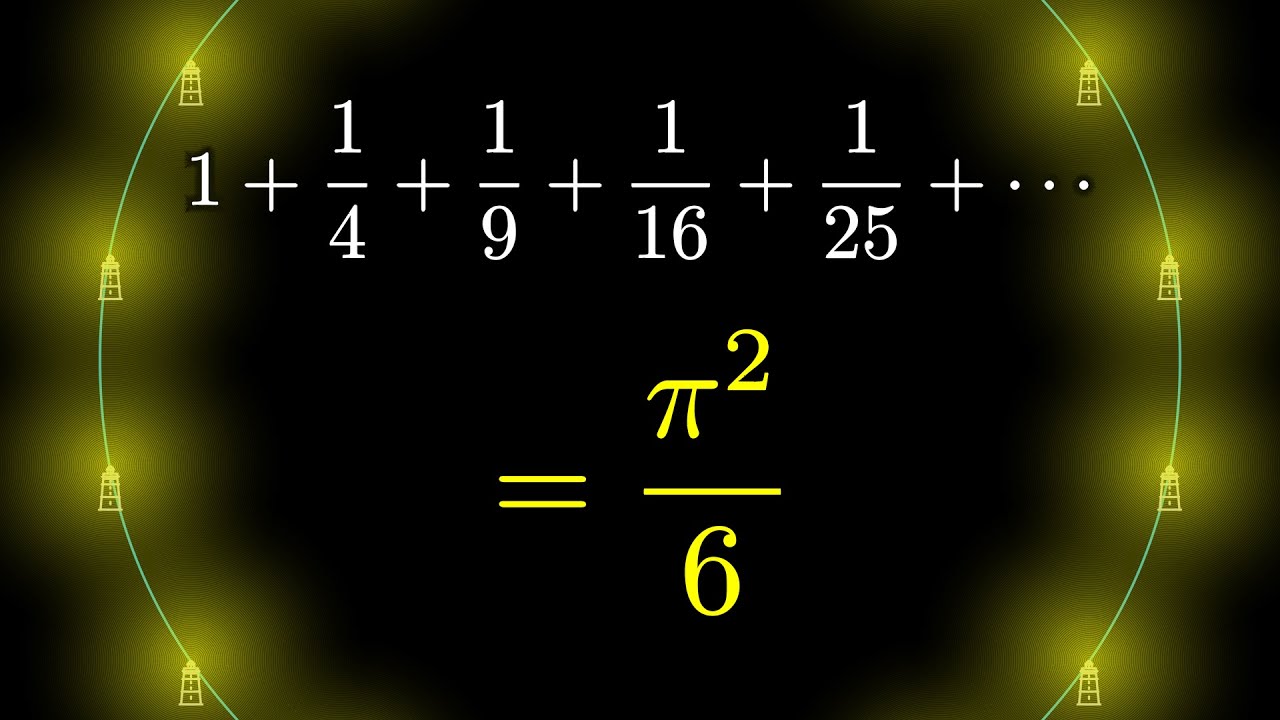



Why Is Pi Here And Why Is It Squared A Geometric Answer To The Basel Problem Youtube



3




The Fourier Series Of F X 0 Pi X 0 Is Chegg Com




2 2 Pi 2 4 Pi Cos Left Frac 2 Pi 2 64 1 Right Cos Left Frac 2 2 Pi 2 64 1 Right Ldots Ldots Cos Left Frac 2 4 Pi 2 64 1 Right 1




Evaluate Integral From P 2 To P 2 X 2 Sin Xdx Cbse Class 12 Sa
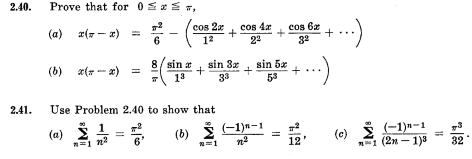



I M Concerned With 2 41 Would I Just Say Chegg Com



1



1
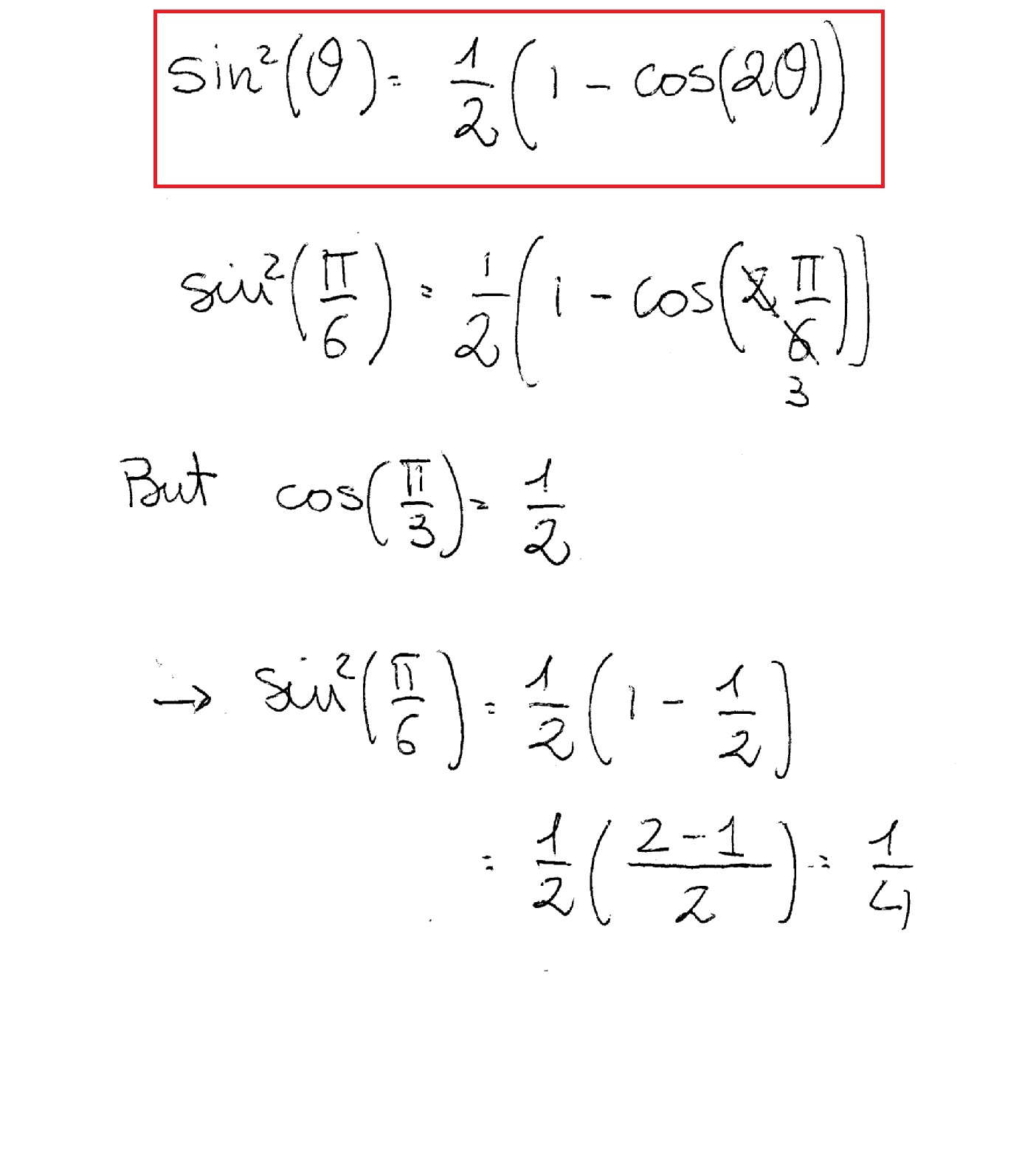



How Do You Use The Half Angle Formula To Simplify Sin 2 Pi 6 Socratic




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11



Biomath Trigonometric Functions
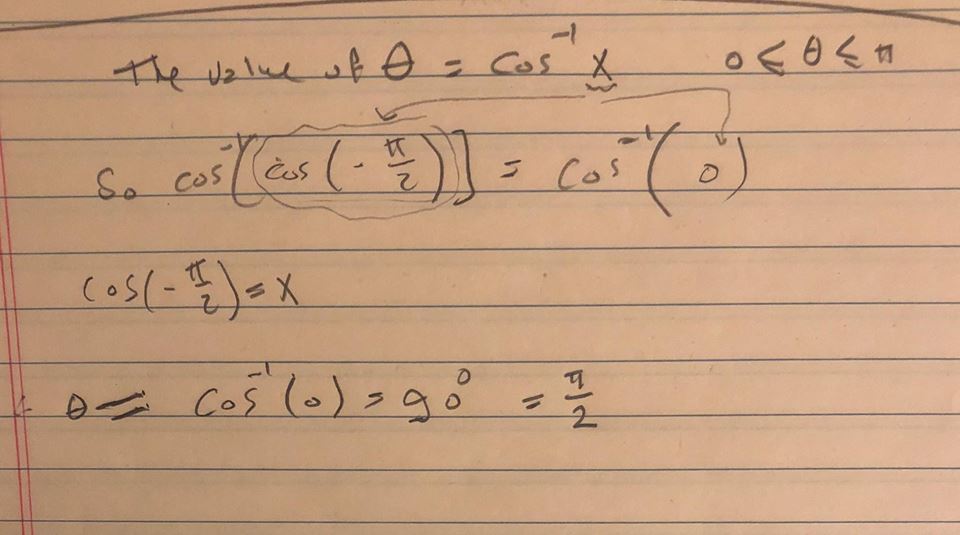



How Do You Evaluate Cos 1 Cos Pi 2 Socratic




Wallis Product Wikipedia




A Geometric Proof Of Zeta 2 Frac Pi 2 6 And Other Integer Inputs For The Zeta Mathematics Stack Exchange




How Pi Was Almost 6 2185 Youtube




Find Exact Value Of Cos 2 Pi 8 Youtube




Sin 2 Frac Pi 6 Cos 2 Frac Pi 3 Tan 2 Frac Pi 4 Frac 1 2 3 Cos 2 Frac Pi 4 Sec Frac 2 Pi 3 5 Tan 2 Frac Pi 3 Frac 29 2




Therefore Y 2 Sin 2 Frac 3 Pi 6



Find The Fourier Series Of F X 0 Pi X 0 Chegg Com



How Do You Find The Value Of Cos Pi 6 Socratic
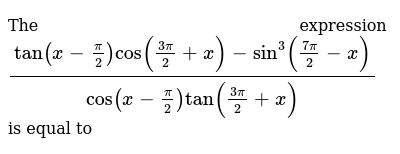



The Expression Tan X Pi 2 Cos 3pi 2 X Sin 3 7pi 2 X Cos X Pi 2 Tan 3pi 2 X Is Equal To
.jpg)



Shifting Angle By P 2 P 3p 2 2p Finding Value Of Trignometric F



How To Calculate The Limit Of Math Frac 2 Sqrt 3 Cos X Sin X 6x Pi Math When Math X Rightarrow Frac Pi 6 Math Quora




The 3 Equal Partition P 1 8 12 2 6 7 3 4 5 9 10 Download Scientific Diagram
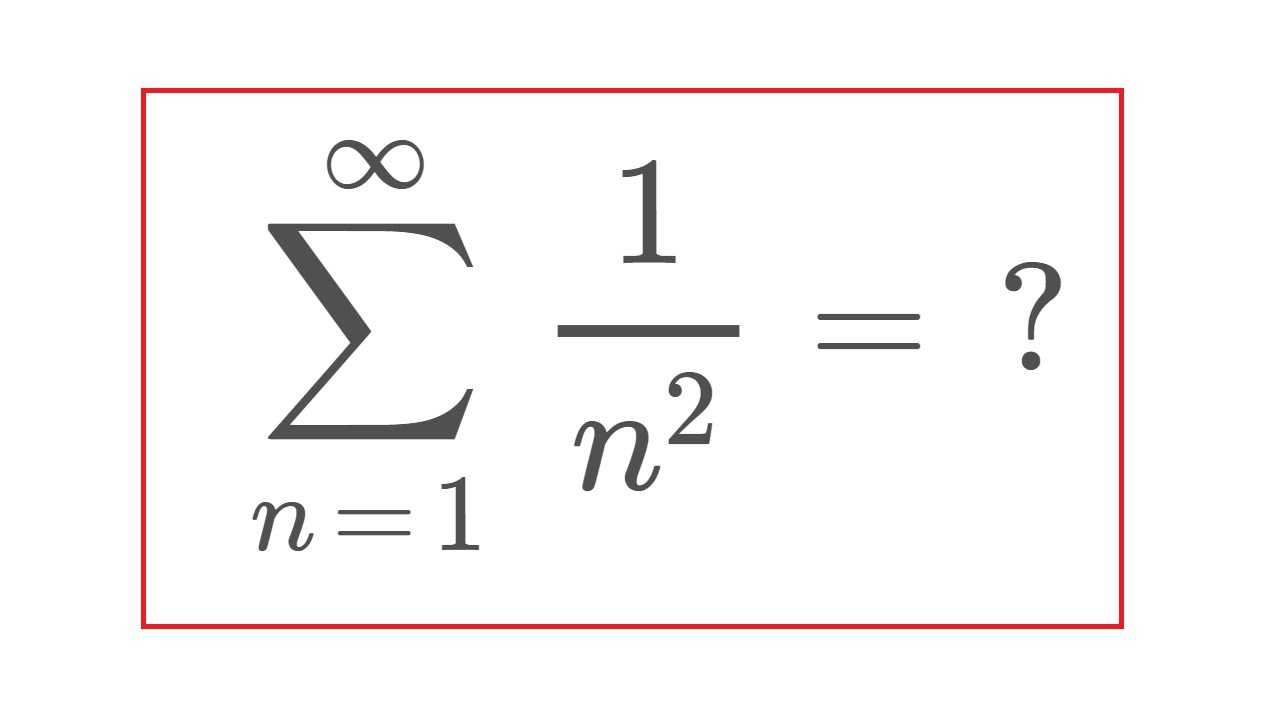



Sum Of 1 N 2 Youtube
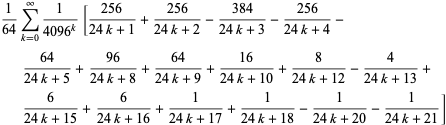



Pi Formulas From Wolfram Mathworld




Basel Problem Wikipedia
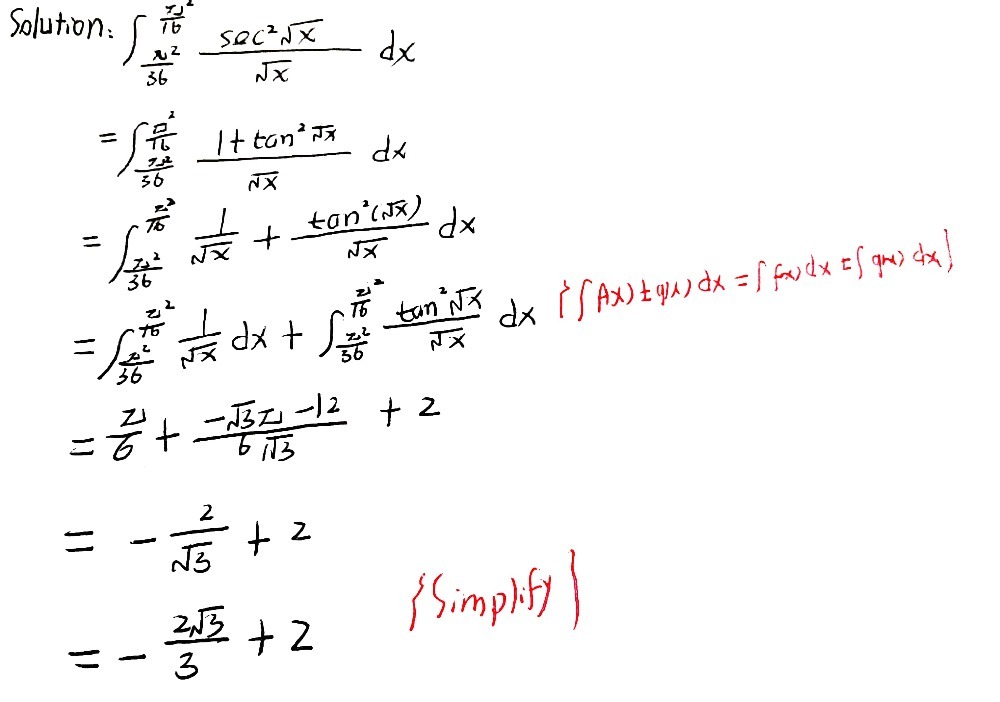



7 T P 2 6 P 2 16frac Sec 2 Square Roo Gauthmath




Limit Trigonometric Function Sin X Pi 6 Sqrt 3 2cosx Youtube
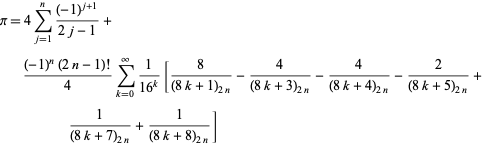



Pi Formulas From Wolfram Mathworld




Basel Problem Wikipedia




Wallis Product Wikipedia
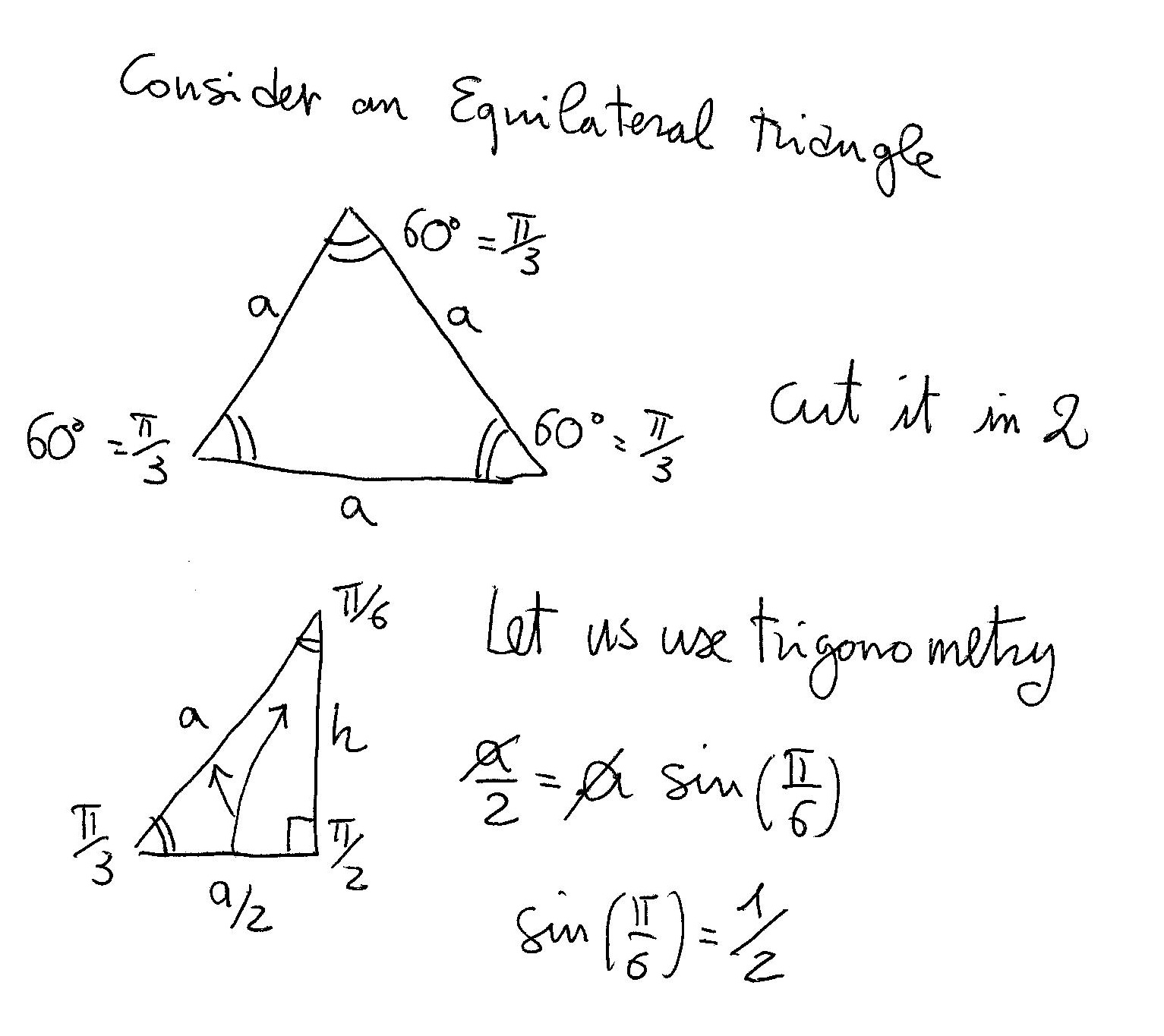



What Is The Value Of Sin Pi 6 Socratic




2 2 Pi Cos Left Frac 2 Pi 2 64 1 Right Cos Left Frac 2 2 Pi 2 64 1 Right Ldots Ldots Cos Left Frac 2 64 Pi 2 64 1 Right 1 Frac 1 16




For X In 0 Pi 2 Prove That Sin X Gt X X 2 6




4 Sin Pi 6 Sin 2 Pi 3 3cos Pi 3 Tan Pi 4 Cose 2 Pi 2 2sec 2 Pi 4




Int 0 Pi 2 Sin 4 X Cos 6 X Dx



0 件のコメント:
コメントを投稿